Distance Measure
Distance Measure describes how we measure distance between two points.
In everyday life, we measure distance between two points using a straight line. This is called Euclidean distance.
There are other useful distance measures, such as Manhattan Distance.
Euclidean distance
Euclidean distance is simply the distance between two points in a straight line. It is also called Pythagorean distance as it can be calculated using the Pythagorean theorem.
The formula for Euclidean distance between two points
(p1,p2)
and
(q1,q2)
is:
Manhattan distance
Manhattan distance (L1 distance) is calculated by summing the absolute differences of the coordinates between two points.
It is usually used in a grid-like system, and is actually simpler to calculate than Euclidean distance as it does not involve square root.
The formula for Manhattan distance between two points
(p1,p2)
and
(q1,q2)
is:
Example
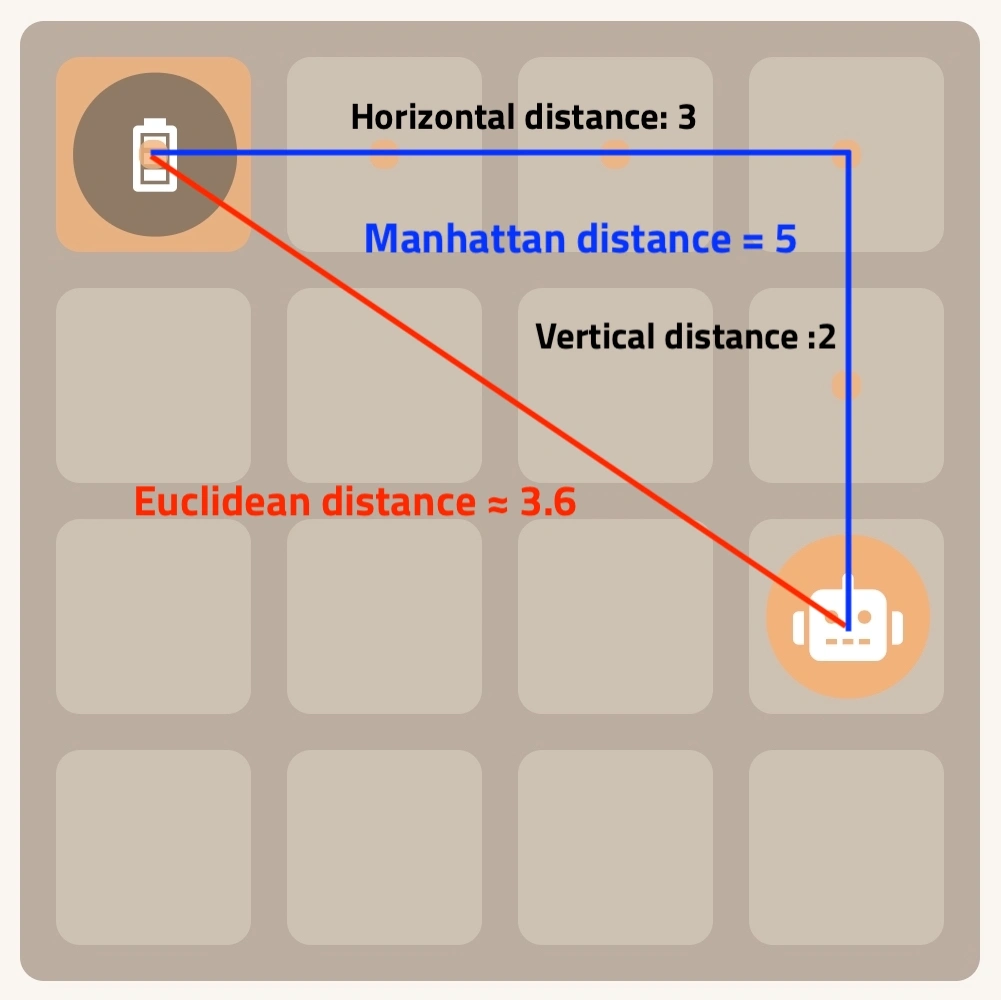
In this AI Simulator: Robot example, we define the
coordinate at bottom-left as
(0,0). The
robot is at
(3,1), the
battery cell is at
(0,3).
The Manhattan distance between the robot and the battery cell is 5. This is calculated by summing the absolute difference in horizontal direction (3) and vertical direction (2).
The Euclidean distance between the robot and the battery cell is approximately 3.6. This is calculated using the Pythagorean theorem, by taking square root of 13, which is sum of horizontal distance squared (3*3) and vertical distance squared (2*2).
Further readings
Distance Measure
Manhattan distance
Euclidean distance